What is this?
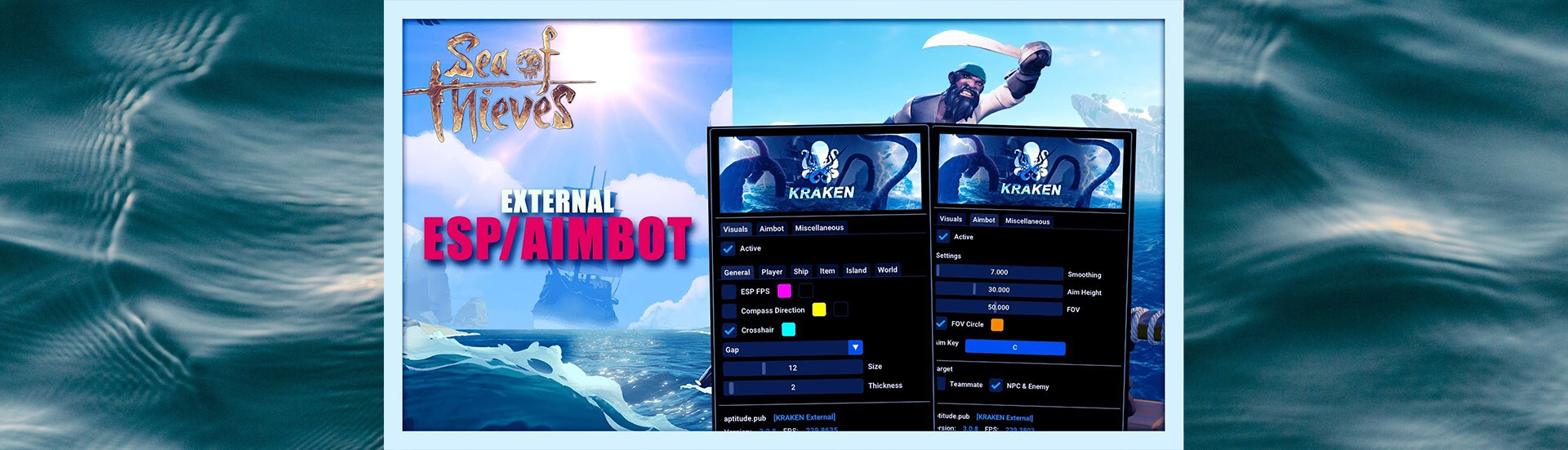
"KRAKEN" was a state-of-the-art gaming software designed to improve targeting accuracy in games involving moving targets and projectiles affected by gravity. Similar to my other open-source project, BF1 External Memory Reading Software, KRAKEN read game memory to gather essential information such as ship speeds and target locations. It used sophisticated algorithms to calculate the optimal firing angle and timing, ensuring successful hits on fast-moving targets. By factoring in elements like target velocity, projectile speed, and gravitational influence, KRAKEN provided gamers with the precision and reliability needed for competitive play. The software was discontinued with the release of Easy Anti-Cheat (EAC) for Sea of Thieves in 2024, which restricted its usage.
Summary
Elevate your gaming skills with KRAKEN, an innovative tool that enhanced your ability to aim accurately in games with complex shooting dynamics. This software predicted target movement and compensated for gravity and speed variations, allowing for perfectly timed and placed shots. With customizable settings for projectile speed and gravitational effects, KRAKEN offered unmatched precision for players looking to boost their performance. While KRAKEN provided a significant competitive edge and consistent shooting success, its development was halted due to the implementation of EAC in Sea of Thieves in 2024, which restricted third-party software usage.
-
Year
2020-2023
-
Client
PythonP Software
-
Services
Reverse Engineering & Physics Simulation
-
Project
KRAKEN: Advanced Projectile Aiming System
Mastering Projectile Aiming in Sea of Thieves with KRAKEN
The Context
KRAKEN is renowned for its array of powerful features, including ESP and exploits like creating an unsinkable ship—game-breaking discoveries that have redefined gameplay strategies. Despite these impactful features, this guide focuses primarily on the cannon prediction functionality, a challenge that combines physics with real-time strategy to enhance accuracy and effectiveness in combat.
The Problem
You're shooting projectiles from a moving cannon to a moving target in Sea of Thieves, where cannon balls move at a constant speed of 57m/s. We assume linear movement of the boats because accounting for acceleration complicates targeting with little gain in accuracy. The maximum range of the cannons is around 450m, depending on the relative velocity between boats.
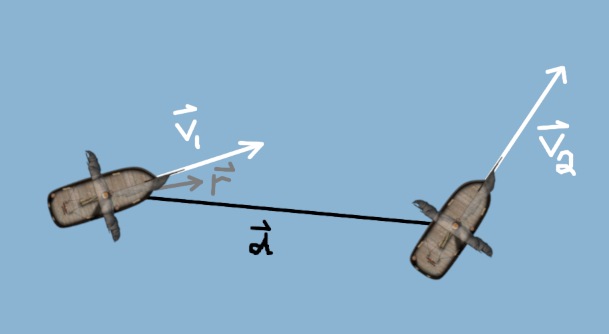
We have to find a vector r where r represents the initial velocity of the projectile, local to the source (cannon). The length of this vector is always equal to the constant traveling speed of the projectile. We can then translate this vector into rotation angles when needed.
The Solution
First, we have to find the time of impact, then we can predict the location of the boat by extrapolating linearly. After that, we can find the shooting angle.
Sea of Quartic Solvers: Finding the Time of Impact
P - Position vector of the target relative to
the position of the source in meters
V - Velocity vector of the target relative to
the velocity of the source in meters
G - Gravity acceleration vector (usually
something like [0, 0, -9.81m/s²])
S - Constant projectile traveling speed
relative to the source in m/s
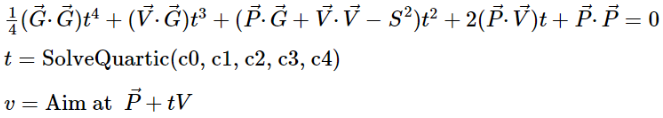
This is a 4th degree polynomial equation, where only t is unknown. We need to find the value of t where the equation is equal to zero, meaning we need to find the root of the equation. This would be a simple task when working with Matlab or a CAS calculator, but finding roots of this equation at runtime is a bit tricky. I couldn't bother reading Wikipedia and making my own solver, so I pasted one from GitHub. I know, very unethical.
// Shamelessly stolen from https://github.com/sidneycadot/quartic/blob/master/solve-quartic.cc
void SolveQuartic(const std::complex<float> coefficients[5], std::complex<float> roots[4]) {
const std::complex<float> a = coefficients[4];
const std::complex<float> b = coefficients[3] / a;
const std::complex<float> c = coefficients[2] / a;
const std::complex<float> d = coefficients[1] / a;
const std::complex<float> e = coefficients[0] / a;
const std::complex<float> Q1 = c * c - 3.f * b * d + 12.f * e;
const std::complex<float> Q2 = 2.f * c * c * c - 9.f * b * c * d + 27.f * d * d + 27.f * b * b * e - 72.f * c * e;
const std::complex<float> Q3 = 8.f * b * c - 16.f * d - 2.f * b * b * b;
const std::complex<float> Q4 = 3.f * b * b - 8.f * c;
const std::complex<float> Q5 = std::pow(Q2 / 2.f + std::sqrt(Q2 * Q2 / 4.f - Q1 * Q1 * Q1), 1.f / 3.f);
const std::complex<float> Q6 = (Q1 / Q5 + Q5) / 3.f;
const std::complex<float> Q7 = 2.f * std::sqrt(Q4 / 12.f + Q6);
roots[0] = (-b - Q7 - std::sqrt(4.f * Q4 / 6.f - 4.f * Q6 - Q3 / Q7)) / 4.f;
roots[1] = (-b - Q7 + std::sqrt(4.f * Q4 / 6.f - 4.f * Q6 - Q3 / Q7)) / 4.f;
roots[2] = (-b + Q7 - std::sqrt(4.f * Q4 / 6.f - 4.f * Q6 + Q3 / Q7)) / 4.f;
roots[3] = (-b + Q7 + std::sqrt(4.f * Q4 / 6.f - 4.f * Q6 + Q3 / Q7)) / 4.f;
}
This also gives us complex roots, which we're not interested in. In my code, I consider that a complex number where the imaginary part is very small is actually a real. If you're not as lazy, you can just make your own or check for negative square roots. You could also use the rule of signs to get the number of solutions beforehand.
Code Implementation
Now that we can solve this monstrosity, let's write some code, shall we.
int AimAtMovingTarget(const SDK::FVector& oTargetPos, const SDK::FVector& oTargetVelocity, float fProjectileSpeed, float fProjectileGravityScalar, const SDK::FVector& oSourcePos, const SDK::FVector& oSourceVelocity, SDK::FRotator& oOutLow, SDK::FRotator& oOutHigh) {
const SDK::FVector v(oTargetVelocity - oSourceVelocity);
const SDK::FVector g(0.f, 0.f, -9.81f * fProjectileGravityScalar);
const SDK::FVector p(oTargetPos - oSourcePos);
const float c4 = g.dot(g) * 0.25f;
const float c3 = v.dot(g);
const float c2 = p.dot(g) + v.dot(v) - (fProjectileSpeed * fProjectileSpeed);
const float c1 = 2.f * p.dot(v);
const float c0 = p.dot(p);
std::complex<float> pOutRoots[4];
const std::complex<float> pInCoeffs[5] = { c0, c1, c2, c3, c4 };
SolveQuartic(pInCoeffs, pOutRoots);
float fBestRoot = std::numeric_limits<float>::max();
for (int i = 0; i < 4; i++) {
if (pOutRoots[i].real() > 0.f && std::abs(pOutRoots[i].imag()) < 0.0001f && pOutRoots[i].real() < fBestRoot) {
fBestRoot = pOutRoots[i].real();
}
}
if (fBestRoot == std::numeric_limits<float>::max())
return 0;
const SDK::FVector oAimAt = oTargetPos + (v * fBestRoot);
return AimAtStaticTarget(oAimAt, fProjectileSpeed, fProjectileGravityScalar, oSourcePos, oOutLow, oOutHigh);
}
My code has a gravity scalar parameter, because cannon balls in Sea of Thieves have around 71% of gravity force applied to them. Now that we have the time of impact (fBestRoot in the code), we can predict where the target is going to be on impact (oAimAt in the code). Now we can aim the projectile at the predicted target position as if the boats weren't moving at all.
Aiming at a Static Target
S - Constant traveling speed of the
projectile in m/s
G - Gravitational acceleration in m/s²
(usually 9.81 m/s²)
x - Distance of the target relative to the
source in m
y - Height of the target relative to the
source in m
However, this formula is in 2D. In order to use it, we'll have to use it along the plane between the source and the target, and then project the results along the X, Y, and Z axis using basic trigonometry.
int AimAtStaticTarget(const SDK::FVector& oTargetPos, float fProjectileSpeed, float fProjectileGravityScalar, const SDK::FVector& oSourcePos, SDK::FRotator& oOutLow, SDK::FRotator& oOutHigh) {
const float g = 9.81f * fProjectileGravityScalar;
const SDK::FVector oDiff(oTargetPos - oSourcePos);
const SDK::FVector oDiffXY(oDiff.X, oDiff.Y, 0.0f);
const float fGroundDist = oDiffXY.magnitude();
const float s2 = fProjectileSpeed*fProjectileSpeed;
const float s4 = s2*s2;
const float y = oDiff.Z;
const float x = fGroundDist;
const float gx = g * x;
float root = s4 - (g * ((gx*x) + (2*y*s2)));
if (root < 0)
return 0;
root = std::sqrtf(root);
const float fLowAngle = std::atan2f((s2 - root), gx);
const float fHighAngle = std::atan2f((s2 + root), gx);
int nSolutions = fLowAngle != fHighAngle ? 2 : 1;
const SDK::FVector oGroundDir(oDiffXY.unit());
oOutLow.FromVector(oGroundDir * std::cosf(fLowAngle) * fProjectileSpeed + SDK::FVector(0.f, 0.f, 1.f) * std::sinf(fLowAngle) * fProjectileSpeed);
if (nSolutions == 2)
oOutHigh.FromVector(oGroundDir * std::cosf(fHighAngle) * fProjectileSpeed + SDK::FVector(0.f, 0.f, 1.f) * std::sinf(fHighAngle) * fProjectileSpeed );
return nSolutions;
}
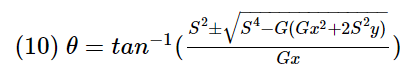
In normal circumstances, there's also a root for a higher angle, but that's not really important since the low angle is almost always preferable.
Conclusion
This method is very accurate, and you basically won't ever
miss a shot. You can aim at any angle using
ACannon::ForceAimCannon, which results in some
pretty funny reactions.
Also, when applied to Sea of Thieves, you should consider the
Z component of the target's velocity to be 0 when shooting
from long distances. The height of the ship doesn't behave
linearly at all, especially over a long duration of time. You
can also use
FBodyInstance::GetPhysicsLinearVelocityAtPoint to
sample the exact cannon velocity when shooting. I wouldn't use
it on the target though, since the angular velocity of the
boat is also not linear over a long period of time.
Another thing to consider is that shooting at the origin of the boat is ineffective. You'll only get good damage if you spread your shots at the bottom of their hull. Plus, the projectiles won't actually hit the target location since the cannon balls would hit the hull before getting there.

To solve this, I use the bounds of the boat, its location, and its forward unit vector to get the red line at the bottom of the hull. Then, we pick a random point on the line and subtract the camera position by it to get the direction of the green line. We multiply it by 8 meters to get the exterior point of the green line of that length. Finally, we can trace the green line to get the impact point, and we'll input this point as the target position into our formulas.

Unfortunately, with the addition of Easy Anti-Cheat (EAC) to Sea of Thieves, my favorite personal project of all time has been discontinued. It's a bittersweet farewell to a project that brought immense joy and learning, but I'm proud of what it achieved while it lasted.


 KRAKEN:
KRAKEN: